
Sample size, variability, and the confidence level affect the widths of confidence intervals. Ok, so you want narrower CIs for their greater precision. What Affects the Widths of Confidence Intervals? Related post: See how confidence intervals compare to prediction intervals and tolerance intervals. If you need to use your sample to find the proportion of data values likely to fall within a range, use a tolerance interval instead. However, it does NOT indicate that 95% of the sample values occur in that range. Remember that these ranges apply only to population parameters, not the data values.įor example, a 95% confidence interval indicates that we can be 95% confident that the parameter is within that range. Related post: Effect Sizes in Statistics Avoid a Common Misinterpretation of Confidence IntervalsĪ frequent misuse is applying confidence intervals to the distribution of sample values. Learn more about how confidence intervals and hypothesis tests are similar. CIs allow you to assess both of these considerations! Learn more about this distinction in my post about Practical vs. Ideally, an estimated effect is both large enough to be meaningful and sufficiently precise for you to trust. In this scenario, consider both the size and precision of the estimated effect. A 2-sample t-test can construct a confidence interval for the mean difference. For example, if you assess a treatment and control group, the mean difference between these groups is the estimated effect size. But you can also create them for regression coefficients, proportions, rates of occurrence (Poisson), and the differences between populations.Ĭonfidence intervals are similarly helpful for understanding an effect size.

You’ll frequently use confidence intervals to bound the sample mean and standard deviation parameters. Confidence intervals place a margin of error around the point estimate to help us understand how wrong the estimate might be. Fortunately, inferential statistics procedures can evaluate a sample and incorporate the uncertainty inherent when using samples. However, the estimates rarely equal the parameter precisely thanks to random sampling error. By using a sample, you can estimate these parameters. Population parameters are typically unknown because it is usually impossible to measure entire populations. Confidence intervals are derived from sample statistics and are calculated using a specified confidence level.
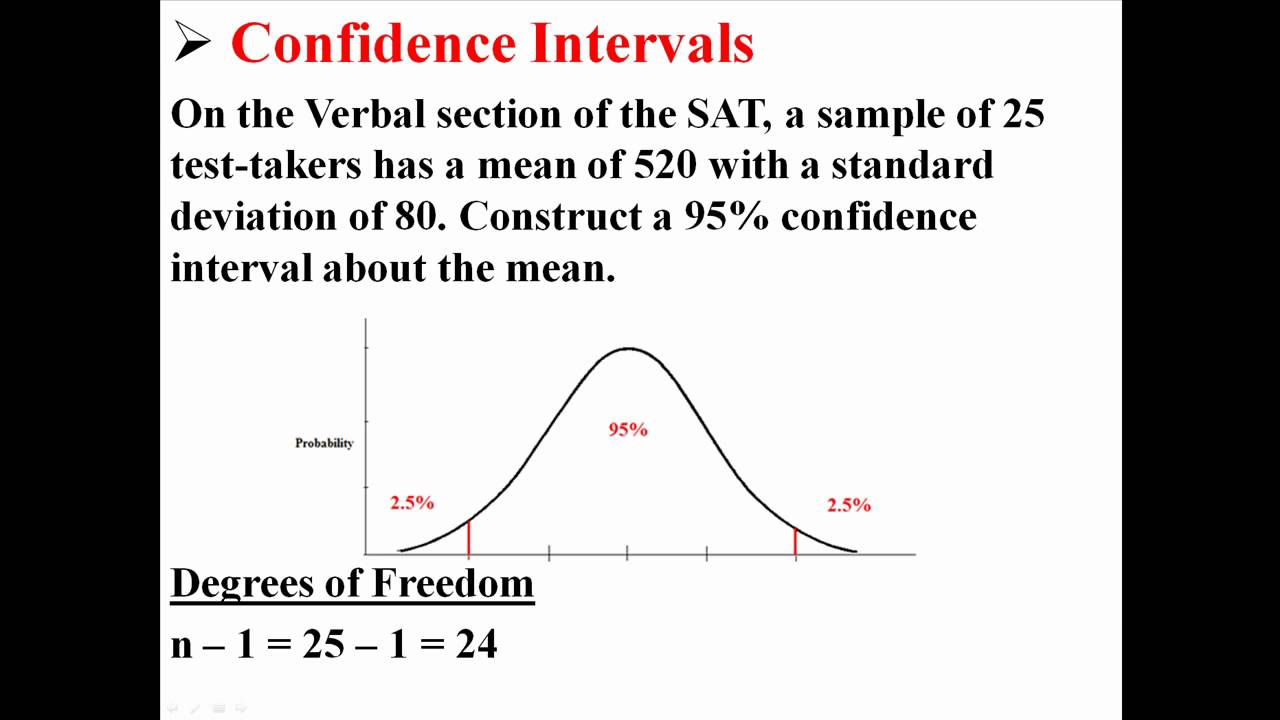
These intervals represent a plausible domain for the parameter given the characteristics of your sample data. A confidence interval (CI) is a range of values that is likely to contain the value of an unknown population parameter.


 0 kommentar(er)
0 kommentar(er)
